The purpose of a system is what it does.
The purpose of a system is what it does. This principle, or
POSIWID, was proposed by
Anthony Stafford Beer, a luminary in operations research and management
cybernetics, also known as systems theory. Although it is dangerous to use this principle to infer intent on the part of individual actors in a system, it is useful for analyzing the
emergent behavior of a system. It certainly cuts through a lot of crap about unintended consequences.
If you don't know this already, I'm a big proponent of the idea of the
egregore, the spirit-of-a-thing, the emergent personality of a system. If one wishes to know the "personality" of a system, that is, its egregore, then one simply observes what the system does:
the purpose of a system is what it does.
There is a site called
Systems Thinking, which describes several
archetypal examples of systems:
Accidental Adversaries,
Fixes that Fail, etc. One classic system is the
Tragedy of the Commons , which also comes up in
game theory (i.e. mathematical microeconomics) and is related to the
Prisoner's Dilemma. The term "Tragedy of the Commons" derives originally from a parable published by William Forster Lloyd in his 1833 book on population:
The parable demonstrates how unrestricted access to a resource such as a pasture ultimately dooms the resource because of over-exploitation. This occurs because the benefits of exploitation accrue to individuals, while the costs of exploitation are distributed between all those exploiting the resource.
Let's look at some classical systems. One of the well-known dyanamical processes in evolutionary biology is the
Lotka-Volterra system, also known as the system of
predator-prey equations, proposed by Alfred J. Lotka in 1925 and Vito Volterra in 1926. Nowdays they are seen as over-simplistic, but they are sufficient to illustrate a point.
The prey are assumed to have an unlimited food supply, and to reproduce exponentially unless subject to predation. The predator population grows in proportion to the probability of a predator meeting a prey, and dies naturally at an otherwise constant rate. The solution depends upon the various rates and initial populations, but a typical solution to the equations looks like this:

Here, blue represents the population of the prey and red represents the population of the predator. The populations oscillate over the course of time, with a spike in prey populations followed by a spike in predator populations. A system where there are two predators for the same prey has a solution that looks something like this (where orange represents the second predator):
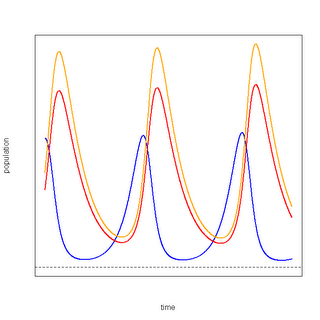
In a system where the competition between two predators intensifies when the prey is scarce, the solution depends on the relative initial populations of the predators and their relative degree of competition. When both predator populations are initially equal and both predators are equally competitive, the system oscillates until it reaches an equlibrium:

When the predators differ in initial population or in the degree of competitiveness, one of the predators can die out:


This is the mathematical intuition behind "survival of the fittest".
All of these systems are archetypal features of the "natural world". However, suppose the rate of prey consumption is large relative to the rate at which the prey replenishes itself. Then there will be a spike in the population of the predator(s), followed by a rapid decrease and re-equilibration:
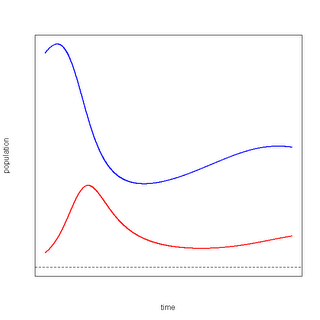
In the limit, when the "prey" cannot replenish itself (or represents a finite resource such as oil), then there will be a spike in population followed by a gradual die-off. One can think of this as the systems picture illustrating the Tragedy of the Commons:

Note that the "resource" need not diminish completely to zero for the predator popluation to become extinct.
Now suppose there is a finite resource and that the intensity of competition between the two predators is inversely proportional to the amount of the resource left. The resulting system looks something like this:
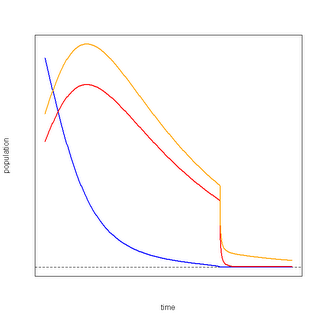
Note the precipitous die-off. The corresponding rate of decline for such a system looks like this:
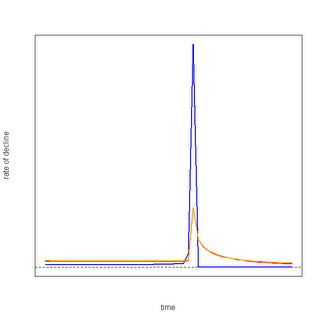
What this means is that there is a huge spike in resource consumption, followed by a corresponding spike in deaths of the predator(s).
The purpose of a system is what it does. In a system where actors are forced to compete for a common finite resource, and to compete more intensely as the resource disappears, the purpose is to kill off the actors in a bloodbath.
Any questions?
Labels: experimental